
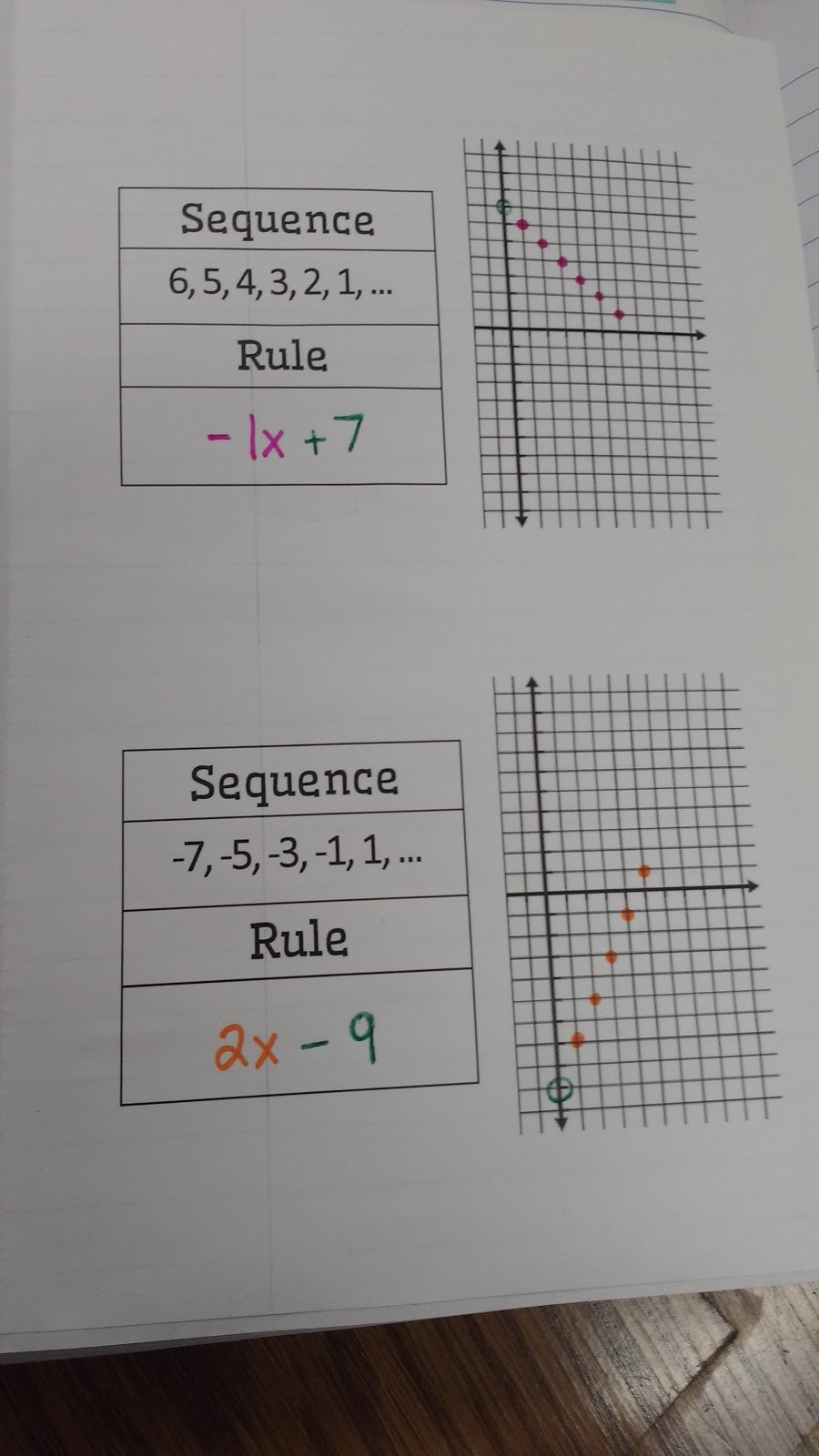
#3 6 arithmetic sequences as linear functions how to#

What students should know and be able to do related to these benchmarks: Know how to use graphing technology to examine these effects.Ĩ.2.2.4 Represent arithmetic sequences using equations, tables, graphs and verbal descriptions, and use them to solve problems.Įxample: If a girl starts with $100 in savings and adds $10 at the end of each month, she will have 100 + 10 x dollars after x months.Ĩ.2.2.5 Represent geometric sequences using equations, tables, graphs and verbal descriptions, and use them to solve problems.Įxample: If a girl invests $100 at 10% annual interest, she will have 100(1.1 x) dollars after x years. Know that the slope equals the rate of change, and that the y-intercept is zero when the function represents a proportional relationship.Įxample: Coordinates used for determining slope must contain integer values.Ĩ.2.2.3 Identify how coefficient changes in the equation f ( x) = mx + b affect the graphs of linear functions.

As students explore other functions such as inverse and exponential functions, it is important that the tables, graphs, equations and situations are continuously compared to what they know about linear functions.Ĩ.2.2.1 Represent linear functions with tables, verbal descriptions, symbols, equations and graphs translate from one representation to another.Ĩ.2.2.2 Identify graphical properties of linear functions including slopes and intercepts. Students can understand more about linear when they compare linear function to other functions. When students identify a situation as linear, it is essential that they are able to identify and make meaning of the slope and y-intercept. Tables, graphs and equations are used to find and interpret solutions to real-world linear situations. Students move from their prior learning of linear relationships that are proportional to all linear functions. In this standard, it is essential for students to be able to move fluidly between different representations of linear functions. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License. Use the information below to generate a citation. Then you must include on every digital page view the following attribution:
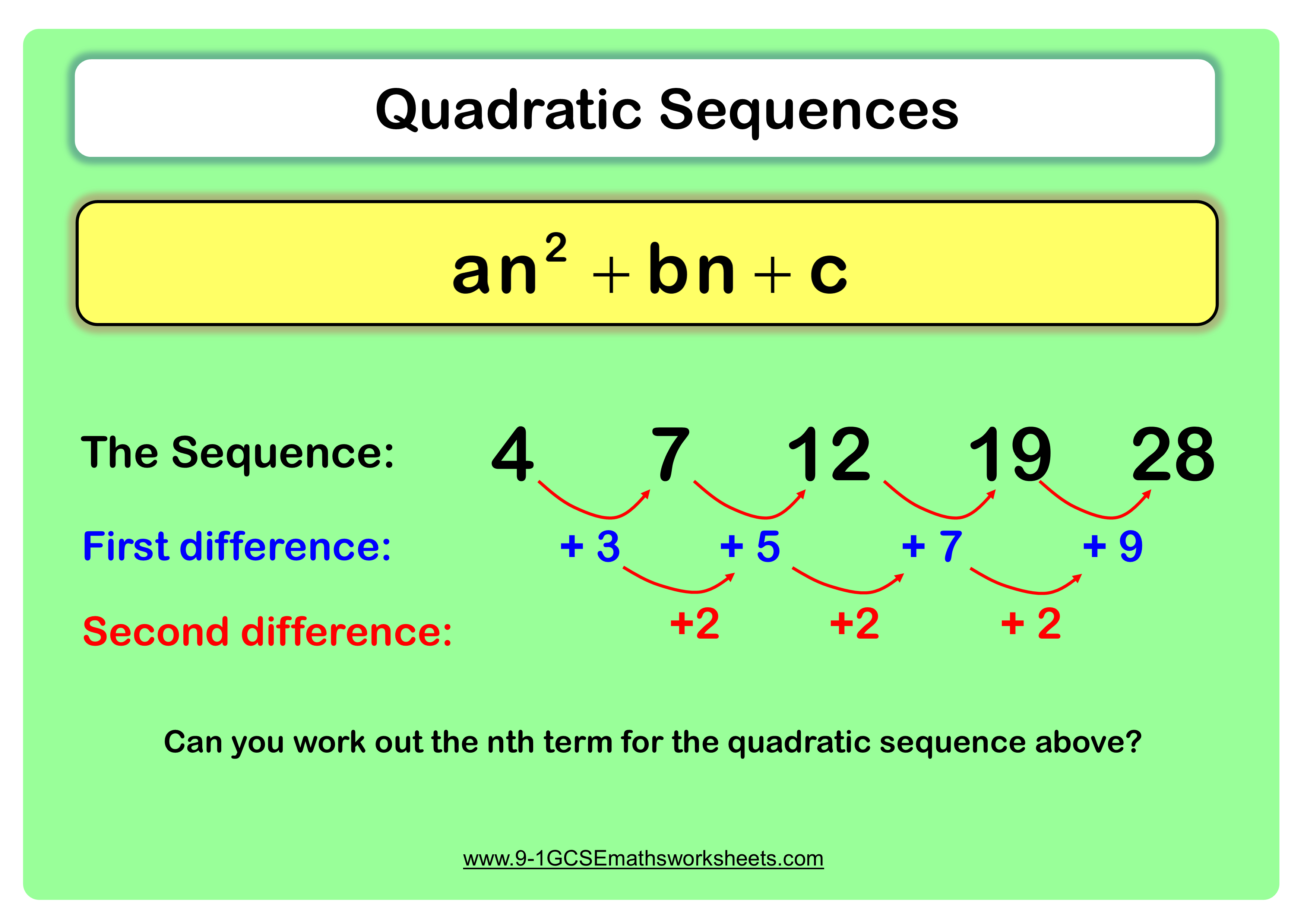
If you are redistributing all or part of this book in a digital format, Then you must include on every physical page the following attribution: If you are redistributing all or part of this book in a print format, Want to cite, share, or modify this book? This book uses the


 0 kommentar(er)
0 kommentar(er)
